- データ構造を一度に再構築して、完全にバランスした状態にする
- 再構築の頻度は、全体の(償却)計算量を増加させない範囲にする
- e.g. 5.2のキュー、ハッシュテーブルのリサイズ
- batched-rebuildingをインクリメンタルにしたもの (償却 => 最悪)
- データ構造の再構築を、通常の操作の合間に差し込んで、少しずつ行っていく(e.g. exec関数呼び出し)
- primary-copy(or warking-copy)とsecondary-copyを保持する
- primary-copy: 再構築作業が(徐々に)適用されるコピー (完了したらオリジナルを置き換え)
- secondary-copy: 再構築中にクライアントからのクエリを処理するためのコピー
- 再構築作業はコルーチンのエミューレート
- データ構造の設計が難しいことが多い
- batched-rebuildingに対して以下の優位性を持つ:
- 永続データ構造に適している
- (償却ではなく)最悪上限を保証する
- e.g. 8.2.1のリアルタイムキュー
- インクリメンタルな遅延データ構造はlazy-rebuilding
- e.g. ストリームを使った遅延キュー(6.3.2)
- global-rebuildingのexec関数呼び出しが、デビットの支払いに対応
- 遅延評価により、二つのコピーの物理メンテが不要となり、より簡潔
- サスペンション群の__支払い済み部分__と__未払部分__のそれぞれが、__working__と__secondary__に対応する
- lazy-rebuildingも永続データ構造に適している
- でも償却上限しか提供しないので、global-rebuildingには劣る?
- schedulingを使えば最悪上限を提供可能
つまり、
- 性質的には
lazy-rebuiling+scheduling==global-rebuilding - 前者(の遅延を利用した手法)の方が、後者(のコルーチンをエミュレートする手法)よりも単純で良いね!
lazy-rebuildingの実例の紹介:
- デック(deques)の実装例:
- デックは両端に要素の追加/削除が行えるキュー
output-restricted-deques(8.4.1)=>banker's deques(8.4.2)=>real-time deques(8.4.3)の流れ- NOTE: output-restricted-dequesは、削除が先頭のみに制限されたデック
- これまでの章を読んでいれば、特に新規性のない内容なので省略
- 以下の流れが把握できていれば問題なし:
償却キュー(5.2)=lazy=>遅延キュー(6.3.2)=schedule=>リアルタイムキュー(7.2)
自然数とリストは、仮想的には同一の構造を持つ:
- 自然数:
datatype Nat = ZERO | SUCC of Nat - リスト:
datatype a List = NIL | CONS of a x a List- リストの場合は、要素を保持するので厳密な型は異なるが、構造は同じ
- 自然数Nは、要素をN個保持するリストに対応する
- 両者に適用される関数も対応している:
- increment <=> cons (ヒープならinsert)
- decrement <=> tail (ヒープならdeleteMin)
- addition <=> append (ヒープならmerge)
- リスト以外のコンテナにも適用可能 (e.g. binomial-heaps)
この類推は、コンテナ抽象の新しい実装をデザインする際に役に立つ:
- 既知の優れた構造(自然数)を利用可能
- デザインの際には「要求される性質を持つ自然数の表現を選択」し、そのコンテナに必要な操作を選択して実装する
- このような方法でデザインされた実装を__数値表現(numerical-representation)__と呼ぶ
本章では以下の二つのコンテナ抽象を扱う:
- ヒープ:
O(1)のincrement/additionが要求される
- ランダムアクセスリスト:
- リストの配列の両方の性質を兼ね備えたデータ構造
O(1)のincrement/decrementが要求される (for list)O(log n)のlookup/updateが要求される (for array)- NOTE: 配列特化(リストの性質が不要)なら、もっと適したデータ構造がある
数をdigit列として表現する記法; 以下、用語:
b(0)...b(n)- b(0): 最下位digit (least-significant-digit)
- b(n): 最上位digit (most-significant-digit)
- 本書では、10進数を除いて
least => mostの順で記述する (! 以降は十進数は太字で表記する)
D(i):b(i)が取り得るdigitの集合 (通常全位置で固定)- e.g. 二進数:
D(i) = {0,1} - ! i番目に位置する木の数に対応
w(i):- i番目の位置のweight
- 数(digit列)の値は、全位置での
b(i) * w(i)の合計 - e.g. 二進数:
w(i) = 2^i - ! i番目に位置する木のサイズ(要素数)に対応
- 冗長(redundant):
- 同じ数を表すdigit列が複数ある数値システムのこと
- e.g.
w(i)=2^i, D(i)={0,1,2}なら__13__は1011と1201と122で表現可能
- コンピュータ上での表現方法は
denseorsparseのいずれか:- dense: 単純なdigitのリスト。zeroを含む (e.g. 9.1のscheduled-binoimal-heaps)
- sparse: denseからzeroを除外したもの。rank or weightの情報が各digitに必要。(e.g. 3.2のbinomial-heaps)
digit集合、weight、dense|sparseが、具体的なpositional-number-systemを決定する上での重要な要因。
positional-number-systemが決まれば、数値を木の列として表現することが可能:
- (denseなら)列のi番目には、サイズが
w(i)の木がb(i)個ある - e.g. __73__は二進表現で1001001: 対応する木の列は
[1,0,0,8,0,0,64](木のサイズのみ記述) - positional-number-systemとしては二進数ベースのものが採用されることが多い
数値表現で使われる木は、通常極めて規則正しい構造を有する:
- 例えば、二進数値表現なら、全ての木のサイズ(要素数)は2の階乗となる
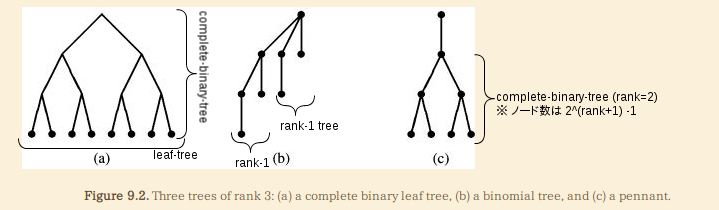
- 以下の三つの種類の木がよく使われる(詳細は図を参照):
- complete-binary-leaf-tree, binomial-tree, pennants
- いずれの木もlink/unlinkが
O(1)で行えることは重要- 数値計算のcarry/borrowに対応
- どれが適切かはデータ構造の要求次第 (e.g.
O(1)のhead関数が必要ならbinomial-trees|pennants)
節の残りではランダムアクセスリストを例に数値表現の適用例を紹介する。
予習:
- 「Binary Random-Access Lists(9.2.1)」は一番ベーシックな構造: cons/tail/headが
O(log n)- headの
O(1)が欲しいなら: 「Zeroless Representations(9.2.2)」 - cons/tailの
O(1)が欲しいなら:- a. 遅延版: 「Lazy Representations(9.2.3)」
- b. 正格版: 「Segmentend Representations(9.2.4)」
- ↑を必要に応じて選択し組み合わせて、具体的なデータ構造を実装する感じとなる
- headの
- 若干アブノーマルな二進数表現でも良いなら、次節の「Skew Binary Numbers(9.3)」も良い選択肢となる
- 簡潔かつ効率的に
O(1)のcons/tail/headが実装可能
- 簡潔かつ効率的に
ランダムアクセスリスト:
- リストの性質(cons,head,tail)と配列的な性質(lookup,update)を兼ね備えたデータ構造
- これを二進数値表現を使って実装する:
- 一番シンプルな
complete-binary-leaf-treesとdenseの組み合わせを採用
- 一番シンプルな
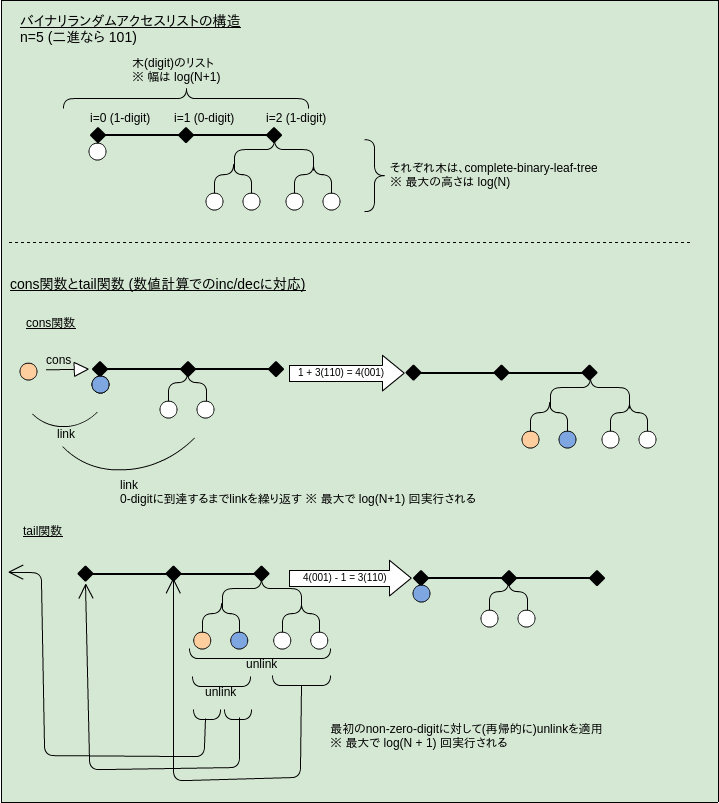
特徴 (詳細は図を参照):
- リストの幅は
log (n + 1)、木の最大の深さはlog n - cons/tail/headは、バイナリ数値操作(inc/dec)に類推を持つ
O(log n)の最悪計算量
- lookup/updateは、バイナリ数値操作に対応物がないが、上記の幅・高さが対数オーダーである恩恵を受ける
- 最初にリストを操作して目的の木を見つける => 次に木を辿って目的の要素を見つける
- どちらも
O(log n)なので、全体も同様
- どちらも
- 以降でも、この性能が改善することはない (! ランダムアクセスを最重要視しているデータ構造ではない)
- 最初にリストを操作して目的の木を見つける => 次に木を辿って目的の要素を見つける
実装:
- まずは対応する数に対する実装を考える:
- 型:
datatype Digit = ZERO | ONE; datatype Nat = Digit List; - inc関数:
fun inc [] = [One] | inc (ZERO::ds) = ONE::ds | inc (ONE::ds) = ZERO::inc ds - dec関数:
fun dec [ONE] = [] | dec (ONE::ds) = ZERO::ds | dec (ZERO::ds) = ONE::dec ds
- 型:
- それを対応するデータ構造の実装に反映する:
- cons/tail: 実装は省略
- 以降も基本的にこの流れで実装が行われる (数の抽象に基づく実装 => 具体的なデータ構造に変換)
- 本質的な構造だけを切り離して考えることができるので分かりやすい
- ただしこの要約では基本的には実装は省略している (ので上の特徴があまり目立たない)
9.2.1のバイナリランダムリストの欠点:
- cons/head/tailが
O(log n)の最悪計算量 - ここではまずheadを
O(1)の最悪計算量にする
O(1)を達成するいくつか方法:
- a. 先頭要素を保持すると特別なフィールドを追加する
- b.
binomial-heapsやpennantsを使う (i.e. 木のルート == 先頭要素、となる) - c. zeroless表現を使う (ここでのトピック)
- lookup/updateが若干速くなるという利点もある (おそらくリストの幅が狭くなるため)
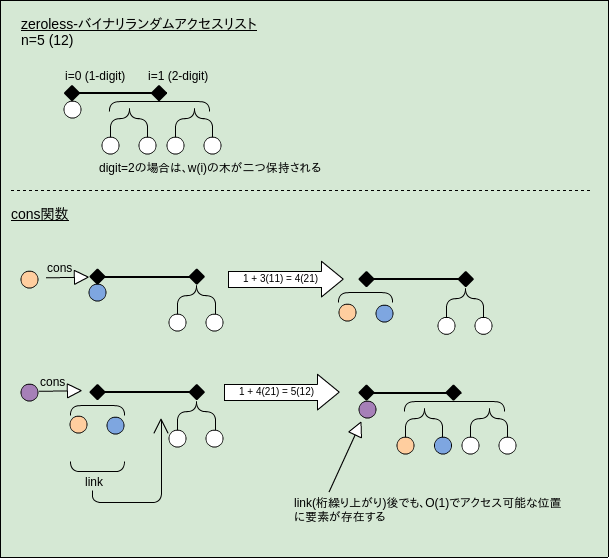
zeroless表現:
{0,1}ではなくD(i)={1,2}でdigitを表現する- e.g. __16__は
2111(00001ではなく)
- e.g. __16__は
- それ以外は以前と同様
- 先頭に常に木が存在するので
O(1)でのheadが可能
cons/tailをO(1)にするには?
- 列の表現をリストからストリームに変更すれば
O(1)の償却計算量が達成可能- consの場合は、0-digitにデビットを割り当てて云々
- 詳細な証明はbinomial-heapsのinsert関数のそれとほとんど同様なので省略
- tailの場合もdigitの役割が逆になるだけで同様 (1-digitにデビットを割り当てる)
- consの場合は、0-digitにデビットを割り当てて云々
- ただし、
- cons/tailを併用すると、どちらかが
O(log n)の償却計算量になってしまう - e.g.
11111のケースで、cons/tailを交互に繰り返す
- cons/tailを併用すると、どちらかが
cons/tailの両方でO(1)を達成するにはどうすれば良いか?
- 何が悪かったのかを考える:
- digitはsafeとdangerousに分類可能
- safe: アクセスしたらそこで処理が終端(terminate)するdigit
- dangerous: アクセスしたら、次のdigitに処理が連鎖するかもしれないdigit
- cons(or tail)だけを考えるとdangerousの発生頻度は
O(1 + 1/2 + 1/4 + 1/8 + ...) = O(1) - 具体的には、
- cons(inc)のdangerous: 最も大きい(= 繰り上げが発生する)digit (i.e. 1)
- tail(dec)のdangerous: 最も小さい(= 繰り下げが発生する)digit (i.e. 0)
- => 両者は相反する! (片方のsafeがもう片方にとってはdangerous)
- digitはsafeとdangerousに分類可能
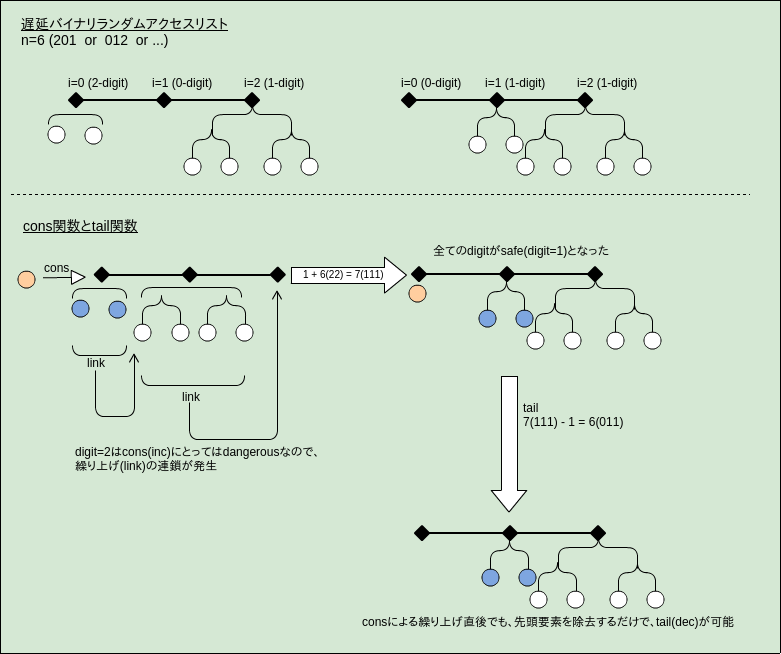
- それなら
D(i) = {0,1,2}をdigitとすれば良い:- 冗長な二進数
- 1がcons(inc)とtail(dec)の両方にとってのsafeなdigit
- carry/borrow時には、このsafeなdigitに遷移するようにする
- inc:
0=>1, 1=>2, 2=>1+繰り上げ(decにとってのdangerousな0に遷移しない) - dec:
1=>0, 2=>1, 0=>1+繰り下げ(incにとってのdangerousな2に遷移しない)
- inc:
- 連鎖が繰り返されなくなった! (e.g. 222 =inc=> 1111 =dec=> 0111)
これで目的のものが得られた:
- cons/tailが
O(1)(償却)- zerolessな
D(i) = {1,2,3}に変更すれば、headもO(1)で実行可能 (演習9.9) - さらにschedulingを使えばcons/tail/headを
O(1)の最悪計算量にすることが可能 (演習9.10)
- zerolessな
- 遅延二進数は、たくさんの他のデータ構造のテンプレートとして使える
- 11章では、これをimplicit-recursive-slowdownと呼ばれるデザインテクニックに汎用化する
! 分量が多い割に新規性のある内容でもないので飛ばしてしまっても良いかもしれない:
- 9.2.3と同等のものを、(遅延なしで)正格に実装するとどうなるか、といった話
- 遅延は「冗長数」で、schedulingは「不変項の維持(のための調整処理)」で代替する
- global-rebuildingでも似たような題材が扱われていた
- 「遅延と正格で等価なものはあるけど、前者の方がシンプルだよね」
cons/tail/headでO(1)の最悪計算量を達成する別の(遅延を使わない)方法を考える:
- そもそも問題なのはcarries/borrowsが連鎖すること
- 冗長数とセグメントを組み合わせることで、この連鎖を避けることが可能
- セグメント:
1111のような連接するdigit列を{4, 1}といったように{連接数、digit値}で表現する方法
- セグメント:
incをO(1)の最悪計算量にする方法を考えてみる:
- まずはセグメントを使わずに話を進める:
- 冗長数を採用:
D(i) = {0,1,2} - 以下の不変項を維持する:
- 取り得るdigit列(正規表現):
(0*1 | 0+1*2)* - 要するに、carryが連鎖する(dangerousな)2-digitが連接するのを避けたい
- 上の不変項を維持すれば
020120112のように、2-digitの前方に必ず0-digitが入るようになる
- 取り得るdigit列(正規表現):
- incの流れ:
-
- まずは普通にインクリメント(simpleInc関数):
0=>1, 1=>2(不変項により先頭digitが2であることはない)
-
- その後、不変更を維持するための調整を適用(fixup関数):
- a. 先頭が
2なら「0にして、次のdigitをインクリメント(不変項により連鎖しない)」 - b. 先頭が
11*2なら「最初の2を0にして、次のdigitをインクリメント(同上)」 - c. それ以外は何もしない
- 要は「0が先行しない2がある場合は、その繰り上げを行う」という処理が必要
- => これさえ行えば、複数の2が連接しない状態を維持可能
-
- 冗長数を採用:
- でも最初の2の前に任意個の1が続く可能性がある(bのケース)なら、どうやってfixup関数を
O(1)で実行する?- そこでセグメントを使う
- 1-digitをセグメントで保持するようにする
- 具体的な型:
datatype Digits = ZERO | ONES of int | TWO - これにより、先頭の1-digit群を
O(1)でスキップ可能となる- 該当コード:
fixup(ONES i :: Two :: ds) = ONES i :: ZERO :: simpleInc(ds)
- 該当コード:
- 無事、inc全体が
O(1)で実行可能となった
- メモ: 遅延版(9.2.3)との類似性についての覚え書き (! 正しいかどうかは不明)
- 冗長数は遅延の一種と考えることができる (おそらく)
inc(1 :: digits)を実行しても、すぐに繰り上げが行われず、後回しにされる1 => 2はサスペンションの作成で、(fixup関数による)2 => 0+繰り上げの遷移はその強制(force)
- 通常のサスペンションと同様に、未評価のものが蓄積するとforceが重くなる (
2222 => 00001) - それを防ぐために毎回少しずつforce(繰り上げ)を行うのが、この節での方法
- schedulingに似ている
- セグメントは、このforceを
O(1)で行うための補助機構 (i.e. 先頭の1-digitsを一度にスキップしたい) - => global-rebuildingとlazy-rebuildingの関係に似ている
- 冗長数は遅延の一種と考えることができる (おそらく)
このテクニックは汎用化が可能:
- 前述の
0,1,2をそれぞれgreen,yellow,redに置き換えるだけ (後は全く同じ) - なぜわざわざ汎用化するのか?
D(i)={0,1,2}以外の数システムに対しても適用可能にするため- 例えば、
- decの
O(1)に対応したければD(i)={0,1,2,3,4}(dangerousの衝突回避)とする必要がある(演習9.12)green=2, yellow=1,3, red=0,5
- headの
O(1)に対応したければD(i)={1,2,3}(zeroless)とする必要がある(演習9.13)
- decの
- これはrecursive-slowdownと呼ばれている:
- 「(狭義には)再帰呼び出しのパターンを工夫して1回の演算で高々定数個のノードのみを処理するようにして、償却計算量ではなく最悪計算量をO(1)とする手法」(by Wikipedia)
- これもいろいろなデータ構造のテンプレートとして使える
- 11章では、遅延版であるimplicit-recursive-slowdownを取り上げる
{lazy,segmented}-binary-numbersでは、inc/decをO(log n)からO(1)に改善する方法を見てきた:
- 三番目の方法を紹介
- 通常は、より簡潔かつ効率的だが、普通(ordinary)の二進数からはよりradicalに離れることになる
skew-binary-numbers:
- w(i):
2^(i+1) - 1(2^iではない) - D(i):
{0,1,2}- e.g. 92 = 002101
- この数値システムは冗長:
- 制限を加えることで冗長ではなくなる
- 「zeroを除いた最下位digitのみがtwoになり得る (
0*2?[01]*)」 - このような数はcanonical-formと呼ばれる (以後はこれのみを仮定)
- 定理9.1: 全ての自然数はcanonical-formのskew-binary-numbersで一意に表現可能
incの話 (decもほぼ同様):
O(1)で実行可能- zeroを除いた最下位が
2なら、それを0にして、次を繰り上げる (制限により繰り上げは連鎖しない)- ! 0番目から順番にインクリメントしていく必要がない (ので
O(1)が簡単に達成可能)
- ! 0番目から順番にインクリメントしていく必要がない (ので
- それ以外なら、最下位digitをインクリメントする:
0 => 1, 1 => 2
- zeroを除いた最下位が
O(1)を達成するためにはsparseである必要がある
skew-binary-numbersを使ったランダムアクセスリストの実装:
- 9.3の数値システムの素直な反映
- sparseな木(digit)のリスト
- 1-digitなら一つの木、2-digitなら二つの木
- 木のサイズ(weight)は
2^(i+1) - 1- complete-binary-treesのノード数と一致しているので、木にはこれを採用
- headを
O(1)にするためには、先頭要素が木のルートにある必要がある- left-to-rightなpreorderで木に要素を保持する
- head/tail/cons:
O(1) - lookup/update:
O(log n)
- リストと配列の両方の性質が欲しいなら、この実装は良い選択
TODO: 図を一つ書いても良いかもしれない
! 軽く流す
skew-binary-numbersとordinary-binary-numbersを組み合わせたヒープ実装を見てみる:
- 前者はincrement(insert)は素晴らしいが、addition(merge)はawkward
- additionには ordinary-binary-numbers を使用する
skew-binomial-tree:
- 各ノードがランクrの範囲の要素を保持する
- ランクと要素数が一意に対応しない
2^r =< |t| =< 2^(i+1) - 1
- 型:
datatype Tree = NODE of int(*rank*) x Elem.T x [Elem.T](* buffer *) x Tree list- バッファリストがある以外は、3.2のbinomial-heapsと同じ構造
skew-binary-heap:
- skew-binary-numbersの木の表現に skew-binomial-tree を採用したヒープ
- 各digit(木)はヒープ順に並んでいる (= 先頭の木のルート要素が一番小さい)
- digitと木の間には、厳格な対応がない(多義性がある)
- e.g. __4__は二進で11だけど、それに対応する木の列には、以下の四通りがある(
{rank, size}の組で記述):[{2, 4}],[{1,2}, {1,2}],[{0,1}, {1,3}],[{0,1}, {0,1}, {1,2}]
- いずれにせよ、ヒープ内の木の数は
O(log n)
- e.g. __4__は二進で11だけど、それに対応する木の列には、以下の四通りがある(
- 大きな利点:
- insertが
O(1)で実行可能(最悪):- skew-binary-numbersのincと同様の流れとなる:
- zeroを除いた最下位digitが2なら「その二つの木をマージ(link)して、挿入要素はバッファリストに追加する」
- それ以外なら「挿入要素のみを含む木を作成して、digit列の先頭に追加する」
- 残りの操作は通常のbinary-binomial-heapsとほぼ同様:
最悪O(log n)- ExplicitMinファンクタを使えばfindMinが
O(1)にできる - 10.2.2では、mergeを
O(1)にする
- insertが
- 二進数以外は忘れられがちだけど、他の数も使える
- weightを変える: 三進数なら
3^i
- weightを変える: 三進数なら
- complete-binary-leaf-trees, binomial-trees, pennantsのいずれも素直に拡張可能
- 基数を増やした場合のトレードオフ:
- 利点: digit数が少なくて済む(e.g. リストの幅が狭くなる)
- 欠点: 各digitが持つ要素が多くなる(e.g. 木は高くなる)
- 計算してみると3か4が良さそう (計算式などは本を参照)
- 2に対して、計算上は16%程度効率的
- ただし、コードが複雑になるので現実的には2の方が速いことが多い
- データ数が極めて大きくなるなら3or4方が5〜10%程度速くなることがある